Frekvensblandare

Skapad: 2024-11-01

Om man tittar i en formelsamling för gymnasiet hittar man under "Trigonometri - Produktformler" eller kanske "Trigonometriska identiteter" följande formel:

2sin α sin β = cos(α - β) - cos(α + β)

Kanske tänker man sig vinklar och trianglar på gymnasiet och inte så mycket signalbehandling, men sinus är sinus och cosinus är fasförskjuten sinus.

Om vi låter α och β beskriva sinusvågor av olika frekvens,

sin α = sin(2πf1t)
sin β = sin(2πf2t)

och förenklar,

sin α = sin f1
sin β = sin f2

så ser vi att multiplikation av två sinusvågor resulterar i två andra sinusvågor vars frekvens är skillnaden respektive summan av frekvensen på de två ingående sinusvågorna.

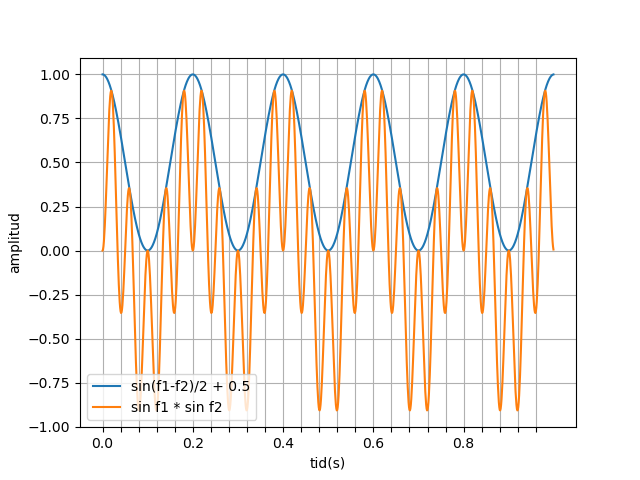
Om vi har två signaler på 15 respektive 10 Hz och multiplicerar dem borde skillnadsprodukten hamna på 5 Hz och ha halva amplituden.

Om vi ritar upp multiplikationen och skillnadsprodukten och förskjuter skillnadsproduktens amplitud och delar in x-skalan i 1/25-dels sekunder så ser vi en intressant bild framför oss:

import matplotlib.pyplot as plt
import numpy as np

f1 = 15
f2 = 10
t = np.arange(0, 1, 1/1000)
s1 = np.cos((2*np.pi*(f1-f2)*t))/2 + 0.5
s2 = np.sin(2*np.pi*f1*t) * np.sin(2*np.pi*f2*t)
plt.plot(t, s1, label="sin(f1-f2)/2 + 0.5")
plt.plot(t, s2, label="sin f1 * sin f2 ")
xs = np.arange(0, 1, 1/25)
plt.xticks(xs, [str(xs[i]) if i%5 == 0 else "" for i in range(xs.shape[0])])
plt.grid()
plt.xlabel('tid(s)')
plt.ylabel('amplitud')
plt.legend()
plt.plot()
plt.savefig('diff.png')

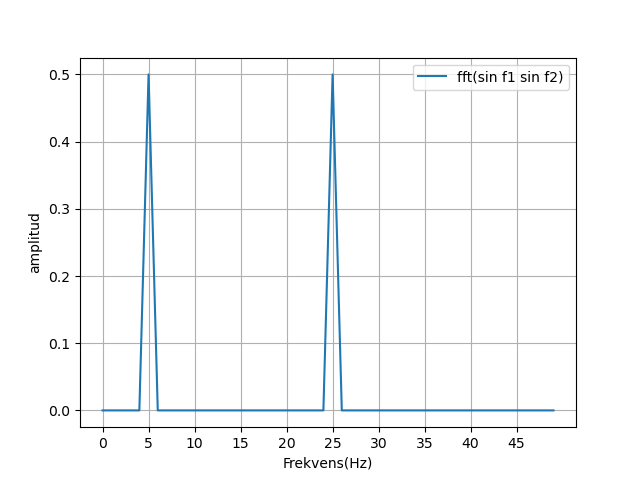
Skillnadsprodukten syns tydligt och vi ser att rutnätet i x-led sammanfaller med en period av den andra framträdande vågrörelsen i bild som ju då är summaprodukten.

Om vi gör en diskret fouriertransform på sin f1 * sin f2 kan vi visualisera det i amplitud som en funktion av frekvens istället för av tid.

import matplotlib.pyplot as plt
import numpy as np
from numpy.fft import fft

N = 1000
f1 = 15
f2 = 10
t = np.arange(0, 1, 1/N)
f_t = np.sin(2*np.pi*f1*t) * np.sin(2*np.pi*f2*t)
ff_t = fft(f_t)
ft = np.linspace(0, 49, 50)
plt.plot(ft, 2.0/N * np.abs(ff_t[:50]), label="fft(sin f1 sin f2)")
plt.xticks(np.arange(0, 50, 5))
plt.xlabel('frekvens(Hz)')
plt.ylabel('amplitud')
plt.grid()
plt.legend()
plt.plot()
plt.savefig('freqs.png')

TODO: Sinusvåg plus fyrkantsvåg